
เมื่อพูดถึงงานเศรษฐศาสตร์วิศวกรรมแล้ว ก็มักจะเป็นงานที่เกี่ยวข้องกับการวิเคราะห์ทางการเงินในงานวิศวกรรมหรือโครงการต่าง ๆ ทางอุตสาหกรรม เช่น การวิเคราะห์การลงทุนในโครงการ, การหาระยะเวลาคืนทุนของโครงการ, การหาระยะเวลาที่ดีที่สุดในการเปลี่ยนเครื่องจักร เป็นต้น โดยผู้ที่ทำการวิเคราะห์หรือมีหน้าที่ที่ต้องตัดสินใจนั้น จะต้องเลือกในสิ่งที่คุ้มค่ากับเงินที่จะเสียไป อาจจะอยู่ในรูปมูลค่าเงินปัจจุบันที่มีกำไรมากที่สุด หรือมีค่าใช้จ่ายน้อยที่สุด, ระยะเวลาคืนทุนของโครงการที่เร็วที่สุด, หรือโครงการที่มีผลประโยชน์ตอบแทนมากที่สุด
|
ผศ.ปรีชา เกรียงกรกฎ |
| . |
|
|
| . |
|
เมื่อพูดถึงงานเศรษฐศาสตร์วิศวกรรมแล้ว ก็มักจะเป็นงานที่เกี่ยวข้องกับการวิเคราะห์ทางการเงินในงานวิศวกรรมหรือโครงการต่าง ๆ ทางอุตสาหกรรม เช่น การวิเคราะห์การลงทุนในโครงการ, การหาระยะเวลาคืนทุนของโครงการ, การหาระยะเวลาที่ดีที่สุดในการเปลี่ยนเครื่องจักร เป็นต้น |
| . |
|
โดยผู้ที่ทำการวิเคราะห์หรือมีหน้าที่ที่ต้องตัดสินใจนั้น จะต้องเลือกในสิ่งที่คุ้มค่ากับเงินที่จะเสียไป อาจจะอยู่ในรูปมูลค่าเงินปัจจุบันที่มีกำไรมากที่สุด หรือมีค่าใช้จ่ายน้อยที่สุด, ระยะเวลาคืนทุนของโครงการที่เร็วที่สุด, หรือโครงการที่มีผลประโยชน์ตอบแทนมากที่สุด และอื่น ๆ ในลักษณะทำนองเช่นเดียวกันนี้ เป็นต้น |
| . |
|
ข้อสังเกตหนึ่งในการศึกษางานเศรษฐศาสตร์วิศวกรรมโดยทั่วไปแล้วนั้น ค่าตัวเลขต่าง ๆ ที่เกี่ยวข้องกับการเงิน อาทิเช่น กระแสเงินสดรับหรือจ่าย, อัตราดอกเบี้ย จะเป็นค่าแบบแน่นอนเพียงค่าเดียว (Deterministic) เมื่อนำค่าที่แน่นอนเหล่านี้ไปวิเคราะห์คำนวณทางเศรษฐศาสตร์วิศวกรรมแล้ว จะได้คำตอบที่แน่นอนเพียงค่าเดียวเช่นกัน |
| . |
|
แต่ถ้าพิจารณาในเชิงของความหมายแล้วจะพบว่าคำตอบที่แน่นอนเพียงค่าเดียวนั้น เป็นค่าที่ไม่แน่นอน หรือเป็นเพียงค่าโดยประมาณเท่านั้น ดังนั้นถ้าต้องการให้ค่าที่ไม่แน่นอนนี้มีความแน่นอน หรือแม่นยำมากยิ่งขึ้น ก็ต้องใช้เทคนิควิธีการอื่นมาช่วย ซึ่งหนึ่งในวิธีการที่จะกล่าวต่อไปนี้ก็คือ ทฤษฎีคลุมเครือ (Fuzzy) เป็นทฤษฎีที่กล่าวถึงกรณีปัญหาที่มีความไม่แน่นอน |
| . |
|
ทฤษฎีนี้ก็มีการนำไปประยุกต์ใช้ในงานต่าง ๆ มากมาย เช่น งานทางด้านไฟฟ้า, งานอิเล็กทรอนิกส์, งานจัดการด้านผลิตสินค้า เป็นต้น ซึ่งทฤษฎีคลุมเครือนี้ก็สามารถนำมาประยุกต์ใช้ในงานเศรษฐศาสตร์วิศวกรรมได้เช่นกัน ดังนั้นเพื่อให้เห็นภาพและเข้าใจในเรื่องนี้มากยิ่งขึ้น ในบทความนี้จะมีการแสดงตัวอย่างการคำนวณประกอบด้วย |
| . |
| Fuzzy Numbers |
|
Zadeh L.A. (1965) เป็นคนนำเสนอทฤษฎี Fuzzy Sets เป็นคนแรก ซึ่งเป็นการเปลี่ยนความรู้สึกคลุมเครือ, ไม่แน่ใจของมนุษย์ ไปอยู่ในรูปแบบเชิงตัวเลข ซึ่งสามารถนำมาวิเคราะห์ทางคณิตศาสตร์ได้ โดยตัวแบบทางคณิตศาสตร์ของ Fuzzy มีอยู่หลายรูปแบบ ดังที่แสดงในรูปที่ 1 ดังนี้ |
| . |
|
|
|
รูปที่ 1 ตัวอย่างรูปแบบทางคณิตศาสตร์ของตัวแบบ Fuzzy Number |
| . |
|
จากรูปที่ 1 ได้แสดงตัวอย่างตัวแบบทางคณิตศาสตร์ของ Fuzzy จำนวน 7 รูปแบบ คือ |
| . |
|
เนื่องจากรูปแบบ Fuzzy Number ที่นิยมนำมาใช้กันมาก ได้แก่ แบบสามเหลี่ยม (Triangular Fuzzy Number: TFN) ดังนั้นในบทความนี้จะกล่าวถึงเฉพาะแบบสามเหลี่ยมเท่านั้น ซึ่งมีรายละเอียดต่าง ๆ ดังต่อไปนี้ |
| . |
|
|
|
รูปที่ 2 รูปแบบสามเหลี่ยม (Triangular Fuzzy Number: TFN) |
| . |
| เงื่อนไขและสมมติฐานของ Triangular Fuzzy Number (TFN) |
|
จากรูปที่ 2 อธิบายได้ดังนี้ |
| . |
|
a1 = ค่าน้อยที่สุด ที่จะเป็นไปได้ (Smallest Possible Value) |
| . |
|
• ความสัมพันธ์ระหว่างแกน X กับแกน Y จะเป็นแบบเส้นตรง |
| . |
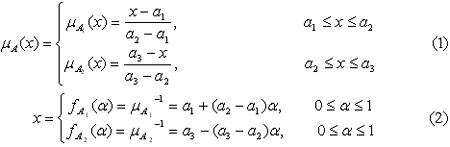 |
| . |
| • ค่า Aสามารถเขียนในรูปแบบ |
| . |
|
• จากสมการที่ (3) มีความหมายคือ |
| . |
| การนำ Triangular Fuzzy Numbers ไปใช้ในงานเศรษฐศาสตร์วิศวกรรม |
| กรณีหามูลค่าเงินปัจจุบัน (Net Present Value: NPV) |
|
ในการศึกษางานเศรษฐศาสตร์วิศวกรรม โดยทั่วไปแล้วกระแสเงินสดรับหรือจ่าย, อัตราดอกเบี้ย จะเป็นค่าแบบแน่นอนเพียงค่าเดียว (Deterministic) แต่ถ้าเป็นกรณีแบบไม่แน่นอน หรือคลุมเครือ (Fuzzy) แล้ว ค่าต่าง ๆ ดังกล่าวจะถูกแจกแจงออกเป็น 3 ค่า ตัวอย่างเช่น ถ้ากล่าวถึงอัตราดอกเบี้ย (r %) จะมีลักษณะดังนี้ |
| . |
| แบบ Deterministic จะมีเพียง 1 ค่า คือ r% |
|
แบบ Fuzzy จะมี 3 ค่า คือ |
| . |
|
ตัวอย่างเช่น อัตราดอกเบี้ยตลอด 3 ปีข้างหน้า |
| . |
|
หมายเหตุ อัตราดอกเบี้ยแบบ Deterministic นี้อาจจะนำเอาค่าของอัตราดอกเบี้ยแบบ Fuzzy ทั้ง 3 ค่าข้างต้น มาหาค่าเฉลี่ยก็ได้ ดังนี้ |
| . |
|
ซึ่งในกรณีนี้ จะเป็นการศึกษาเรื่อง TFN for Economic ดังนั้นจะนำค่าทั้ง 3 ค่าแบบ Fuzzy ข้างต้นนั้น ไปทำการคำนวณด้วยวิธีการ Fuzzy Mathematics ตามกรณีของปัญหาที่กำลังพิจารณา ดังตัวอย่างต่อไปนี้ |
| . |
|
ตัวอย่างที่ 1 Fuzzy Net Present Value of Uncertain Cash Flow |
| . |
| วิธีทำ จากข้อมูลโครงการนำมาเขียน Cash Flow Diagram ได้ดังนี้ |
|
|
|
รูปที่ 3 แสดง Cash Flow Diagram ของตัวอย่างที่ 1 |
| . |
| หามูลค่าเงินปัจจุบัน (Net Present Value; NPV) ของโครงการแห่งนี้จากสูตร |
| . |
| โดยที่แฟกเตอร์ (P/A, r, d, n) สามารถเขียนในอีกรูปแบบได้ดังนี้ |
| . |
| ดังนั้น Membership Function ของ NPV คือ |
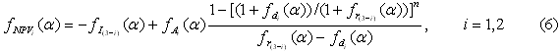 |
| . |
| เขียนในรูปแบบ |
| . |
| โดยที่ |
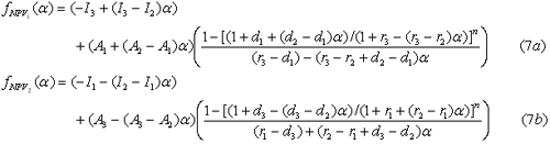 |
| . |
|
มูลค่าเงินปัจจุบันที่ได้จากสูตรนี้จะอยู่ในรูปที่เรียกว่า Approximated Net Present Value หรือ ANPV ซึ่งจะมี 3 ค่าตามรูปแบบ triangular fuzzy number ดังนี้ |
| โดยที่ |
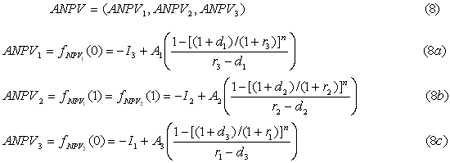 |
| . |
|
ถ้าตัวอย่างโจทย์ปัญหาข้อนี้ มีตัวเลขการเงิน คือ |
| . |
| จะหามูลค่าเงินปัจจุบันได้ดังนี้ แทนค่าในสมการที่ (7a) และ (7b) จะได้ |
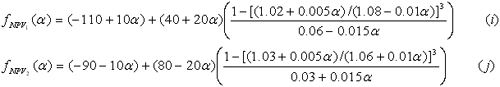 |
| . |
| หาค่า Approximated Net Present Value หรือ ANPV โดยแทนค่า |
|
นั่นคือ |
| . |
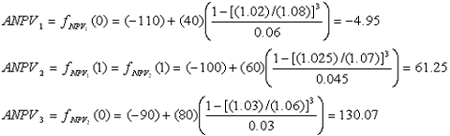 |
| . |
| ถ้านำมูลค่าเงินปัจจุบันที่คำนวณได้นี้มาเขียนเป็นกราฟ จะได้ดังรูปที่ 4 ดังนี้ |
|
|
|
รูปที่ 4 แสดง Triangular Fuzzy Number (TFN) ของมูลค่าเงินปัจจุบันของตัวอย่างที่ 1 |
| . |
|
ข้อสังเกตสำหรับค่า ANPV1 หรือมูลค่าเงินปัจจุบันที่น้อยที่สุดที่จะเป็นไปได้ที่มีค่าเป็นลบนั้น (-4.95 บาท) มีความหมายคือ โครงการนี้มีความเป็นไปได้ที่จะขาดทุนนั่นเอง |
| . |
| กรณีหาระยะเวลาคืนทุน (Pay Back Year: PBY) |
|
จากตัวแบบในหัวข้อมูลค่าเงินปัจจุบันข้างต้น สามารถนำมาประยุกต์ใช้ในกรณีหาระยะเวลาคืนทุนต่อไปได้ ซึ่งจะเป็นการปรับมูลค่าเงินปัจจุบันในสมการที่ (4) ให้เป็นศูนย์ แล้วจัดรูปสมการใหม่จะได้ |
| . |
| . |
| Membership Function ของ PBY คือ |
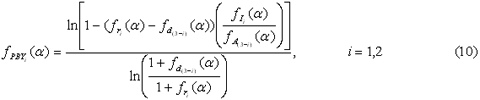 |
| . |
| เขียนในรูปแบบ |
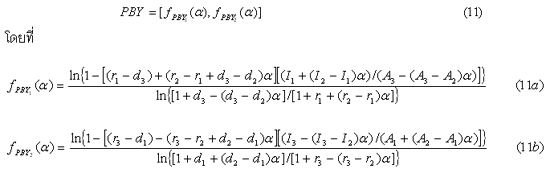 |
| . |
|
ระยะเวลาคืนทุนที่ได้จากสูตรนี้จะอยู่ในรูปที่เรียกว่า Approximated Pay Back Year หรือ APBY ซึ่งจะมี 3 ค่าตามรูปแบบ Triangular Fuzzy Number ดังนี้ |
| . |
|
|
| . |
|
ตัวอย่างที่ 2 Fuzzy Pay Back Year of Uncertain Cash Flow |
|
จงหาระยะเวลาคืนทุนของโครงการแห่งหนึ่ง ที่มีตัวเลขทางการเงินดังนี้ |
| . |
| วิธีทำ นำข้อมูลในโจทย์ไปแทนค่าในสมการที่ (12a), (12b), และ (12c) จะได้ |
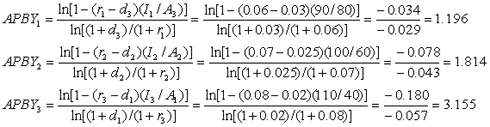 |
| . |
|
นั่นคือ |
| . |
|
|
|
รูปที่ 5 แสดง Triangular Fuzzy Number (TFN) ของระยะเวลาคืนทุนของตัวอย่างที่ 2 |
| . |
| กรณีการเปรียบเทียบโครงการด้วย Fuzzy Net Present Value และ Fuzzy Pay Back Year |
|
ในบางครั้งเมื่อต้องมีการเลือกโครงการที่ดีที่สุดจากทางเลือกที่มีหลายโครงการนั้น ในแง่ของการวิเคราะห์การเงินแล้วก็จำเป็นที่จะต้องโครงการเหล่านั้นจะต้องถูกเปรียบเทียบในฐานเดียวกัน ในที่นี้จะใช้หลักการของมูลค่าเงินปัจจุบันและระยะเวลาคืนทุน โดยมีหลักการเลือกโครงการดังนี้ |
| . |
|
• วิธีมูลค่าเงินปัจจุบัน : ให้เลือกโครงการที่มีมูลค่าเงินปัจจุบัน มากที่สุด |
| . |
| ตัวอย่างที่ 3 Fuzzy Alternatives Decision-Making |
| จงวิเคราะห์เลือกโครงการที่ดีที่สุดจาก 2 โครงการ คือ โครงการ EC-TG และโครงการ BP-TG ตามรายละเอียดการเงินดังนี้ |
|
|
| . |
| • อัตราดอกเบี้ยต่อปี (r %) = (6, 7, 8) % • อัตราเงินเฟ้อต่อปี (d %) = (2, 2.5, 3) % • อายุของโครงการเท่ากับ 15 ปี (เท่ากันทั้ง 2 โครงการ) |
| . |
|
วิธีทำ ในที่นี้จะวิเคราะห์ด้วยมูลค่าเงินปัจจุบัน และระยะเวลาคืนทุน |
| . |
| 1) วิเคราะห์ด้วยวิธีมูลค่าเงินปัจจุบัน ใช้สมการที่ (7a) และ (7b) |
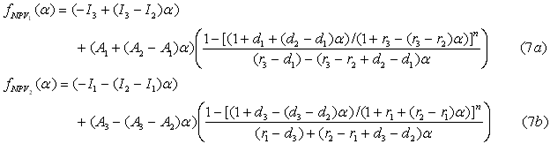 |
|
1.1) หา ANPV ของโครงการ EC-TG |
 |
| . |
| 1.2) หา ANPV ของโครงการ BP-TG แทนค่าตัวเลขทางการเงินลงในสมการที่ (7a) และ (7b) ข้างต้นอีกครั้งจะได้ |
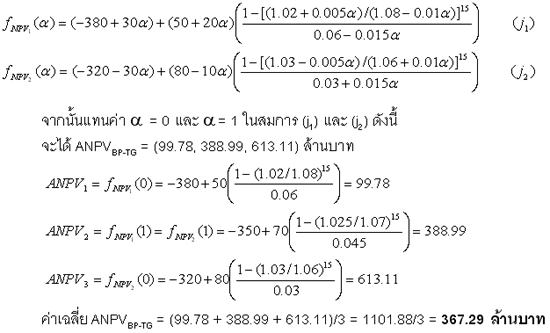 |
| . |
|
2) วิเคราะห์ด้วยวิธีระยะเวลาคืนทุน |
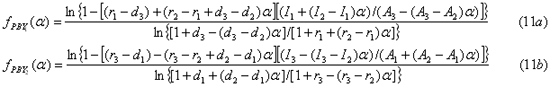 |
| . |
|
2.1) หา APBY ของโครงการ EC-TG |
 |
| . |
|
2.2) หา APBY ของโครงการ BP-TG |
 |
| . |
|
3) สรุปผลการวิเคราะห์ |
|
|
| . |
|
|
|
รูปที่ 6 แสดงการเปรียบเทียบ NPV Membership Function ของโครงการ EC-TG และโครงการ BP-TG |
| . |
|
|
|
รูปที่ 7 แสดงการเปรียบเทียบ PBY Membership Function ของโครงการ EC-TG และโครงการ BP-TG |
| . |
|
จากค่าในตารางและรูปภาพข้างต้น จะเห็นว่า มูลค่าเงินปัจจุบันของโครงการ EC-TG (555.46 ล้านบาท) มีค่ามากกว่าของโครงการ BP-TG (367.29 ล้านบาท) และระยะเวลาคืนทุนของโครงการ EC-TG (6.18 ปี) ก็มีระยะเวลาที่น้อยหรือเร็วกว่าของโครงการ BP-TG (7.01 ปี) ดังนั้นจึงควรเลือกโครงการ EC-TG ตอบ |
| . |
| สรุป |
|
การนำทฤษฎีคลุมเครือ (Fuzzy) ซึ่งเป็นทฤษฎีที่กล่าวถึงกรณีปัญหาที่มีความไม่แน่นอน มาประยุกต์ใช้ในงานเศรษฐศาสตร์วิศวกรรม จะทำให้การวิเคราะห์ปัญหามีความแน่นอน หรือแม่นยำมากยิ่งขึ้น โดยคำตอบที่ได้จากการคำนวณจะมี 3 ค่า คือ ค่าน้อยที่สุดที่จะเป็นไปได้, ค่าที่มีความเป็นไปได้มากที่สุด, และค่ามากที่สุดที่จะเป็นไปได้ ทำให้ผู้ที่ทำการวิเคราะห์หรือผู้ที่มีหน้าที่รับผิดชอบโครงการ เห็นคำตอบของปัญหาได้อย่างครอบคลุม ชัดเจนขึ้น และทำให้การตัดสินใจในปัญหานั้น มีความมั่นใจและมีประสิทธิภาพมากยิ่งขึ้นด้วยเช่นกัน |
| . |
|
และนอกเหนือจากการนำทฤษฎีคลุมเครือ (Fuzzy) นี้ไปใช้ในกรณีหามูลค่าเงินปัจจุบัน และระยะเวลาคืนทุนของโครงการตามตัวอย่างข้างต้นแล้ว เรายังสามารถนำไปประยุกต์ใช้ในการแก้ไขปัญหาในลักษณะอื่น ๆ ได้อีก เช่น การพิจารณางบประมาณเงินลงทุนในโครงการที่ไม่แน่นอน, การใช้อัตราส่วนผลประโยชน์ต่อค่าใช้จ่ายแบบทฤษฎีคลุมเครือในการเลือกโครงการ, การวิเคราะห์หามูลค่าเงินเทียบเท่ารายปีแบบทฤษฎีคลุมเครือ, หรือการหามูลค่าเงินในอนาคตกรณีที่มีความไม่แน่นอนเกิดขึ้น เป็นต้น |
| . |
|
เอกสารอ้างอิง |
|
1) วันชัย ริจิรวนิช และ ชอุ่ม พลอยมีค่า , “เศรษฐศาสตร์วิศวกรรม”, โรงพิมพ์จุฬาลงกรณ์มหาวิทยาลัย, 2531. |
สงวนลิขสิทธิ์ ตามพระราชบัญญัติลิขสิทธิ์ พ.ศ. 2539 www.thailandindustry.com
Copyright (C) 2009 www.thailandindustry.com All rights reserved.
ขอสงวนสิทธิ์ ข้อมูล เนื้อหา บทความ และรูปภาพ (ในส่วนที่ทำขึ้นเอง) ทั้งหมดที่ปรากฎอยู่ในเว็บไซต์ www.thailandindustry.com ห้ามมิให้บุคคลใด คัดลอก หรือ ทำสำเนา หรือ ดัดแปลง ข้อความหรือบทความใดๆ ของเว็บไซต์ หากผู้ใดละเมิด ไม่ว่าการลอกเลียน หรือนำส่วนหนึ่งส่วนใดของบทความนี้ไปใช้ ดัดแปลง โดยไม่ได้รับอนุญาตเป็นลายลักษณ์อักษร จะถูกดำเนินคดี ตามที่กฏหมายบัญญัติไว้สูงสุด